Mật mã đường cong Elliptic (ECC) là gì?

Việc sử dụng ngày càng phổ biến các dịch vụ đám mây và mạng xã hội  đồng nghĩa với việc thông tin cá nhân có khả năng bị rò rỉ khi  lưu trữ trên internet. Để bảo vệ thông tin, mã hóa dữ liệu là chìa khóa và được xem là một phương pháp hiệu quả và được sử dụng rộng rãi. Trong số nhiều thuật toán mã hóa khác nhau, mật mã đường cong Elliptic (ECC) là thuật toán mã hóa mạnh nhất, nhưng cũng là thuật toán phức tạp nhất. Hãy cùng BlockchainWork khám phá mật mã đường cong ở bài viết ngay sau đây nhé!

Tìm hiểu về Private key/ Public Key

Trước hết, bạn cần biết private key và public key của mình. Khóa riêng là khóa mà chỉ bạn biết và khóa công khai là khóa chung được ghép nối với khóa riêng của bạn. Trong công nghệ chuỗi khối, khóa riêng và khóa công khai trong mật mã khóa công khai được sử dụng như một phương thức xác nhận người gửi dữ liệu được gọi là “chữ ký điện tử”. 

>> Xem thêm: Khóa công khai và khóa riêng là gì? 2 loại khóa này khác nhau như thế nào?

Vậy khóa riêng và khóa công khai được tạo như thế nào? Đầu tiên, đối với khóa riêng, hãy tạo ngẫu nhiên một số lượng lớn. Vì người ta cho rằng khóa riêng tư chỉ được biết bởi chính người đó nên không cần phải quá chú ý về việc người khác không thể nhìn thấy. Vấn đề là khóa công khai. Khóa công khai được tạo bằng cách thực hiện một số tính toán trên khóa riêng, nhưng khóa công khai là thông tin được phát trên mạng và được mở cho công chúng. Vì vậy, phương pháp tính toán phải được thiết kế để gây khó khăn trong việc tính toán ngược khóa riêng từ khóa công khai. Thuật toán tính toán này là phương pháp mã hóa sử dụng đường cong elip (elliptic curve cryptography).

Đường cong elip là gì?

Đường cong elip là đường cong phẳng được xác định bởi phương trình có dạng dưới đây:

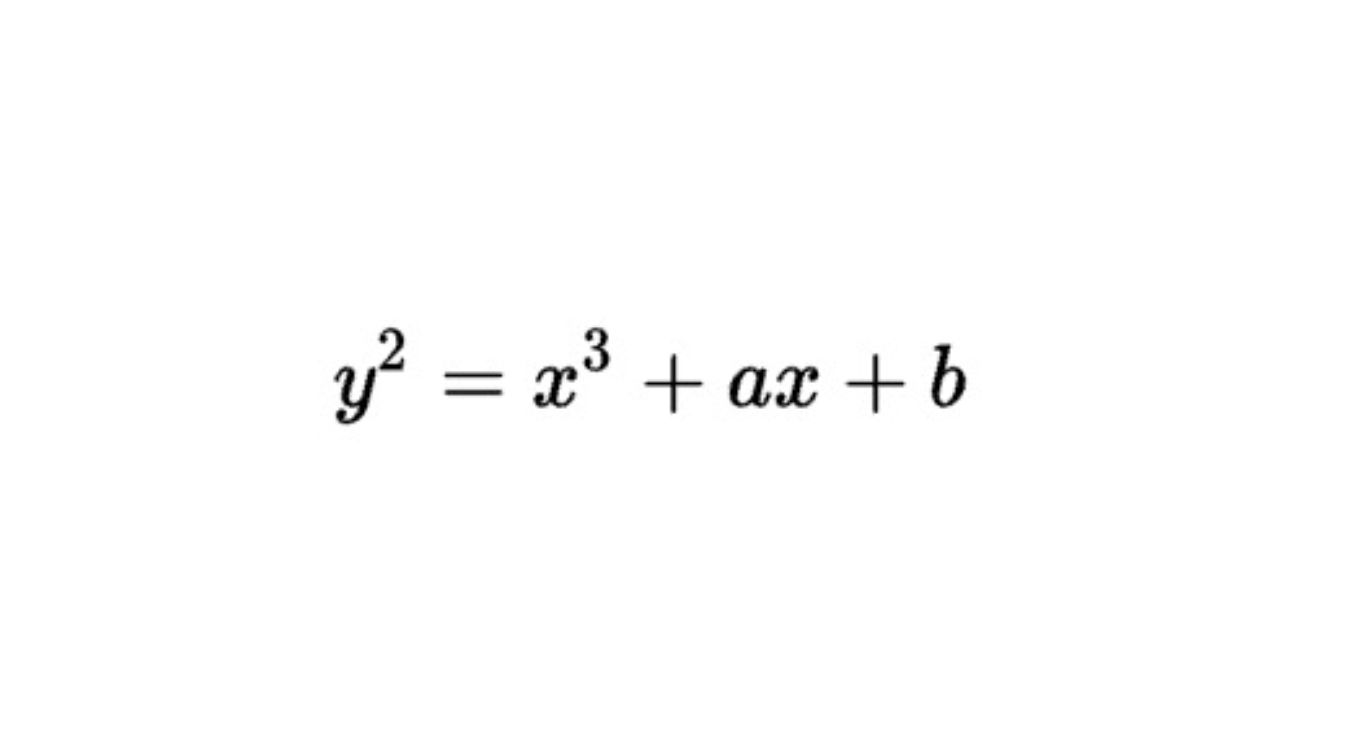
Hình minh hoạ phương trình đường cong elip

Bằng cách thay đổi các giá trị của a và b, có thể thu được các hình dạng đường cong khác nhau như hình bên dưới. Nhưng đường cong này rõ ràng không phải là hình elip. Từ “hình elip” bắt nguồn từ một thứ khác, đường cong hình elip này được sử dụng trong thuật toán mã hóa sẽ được giải thích ở phần sau. 

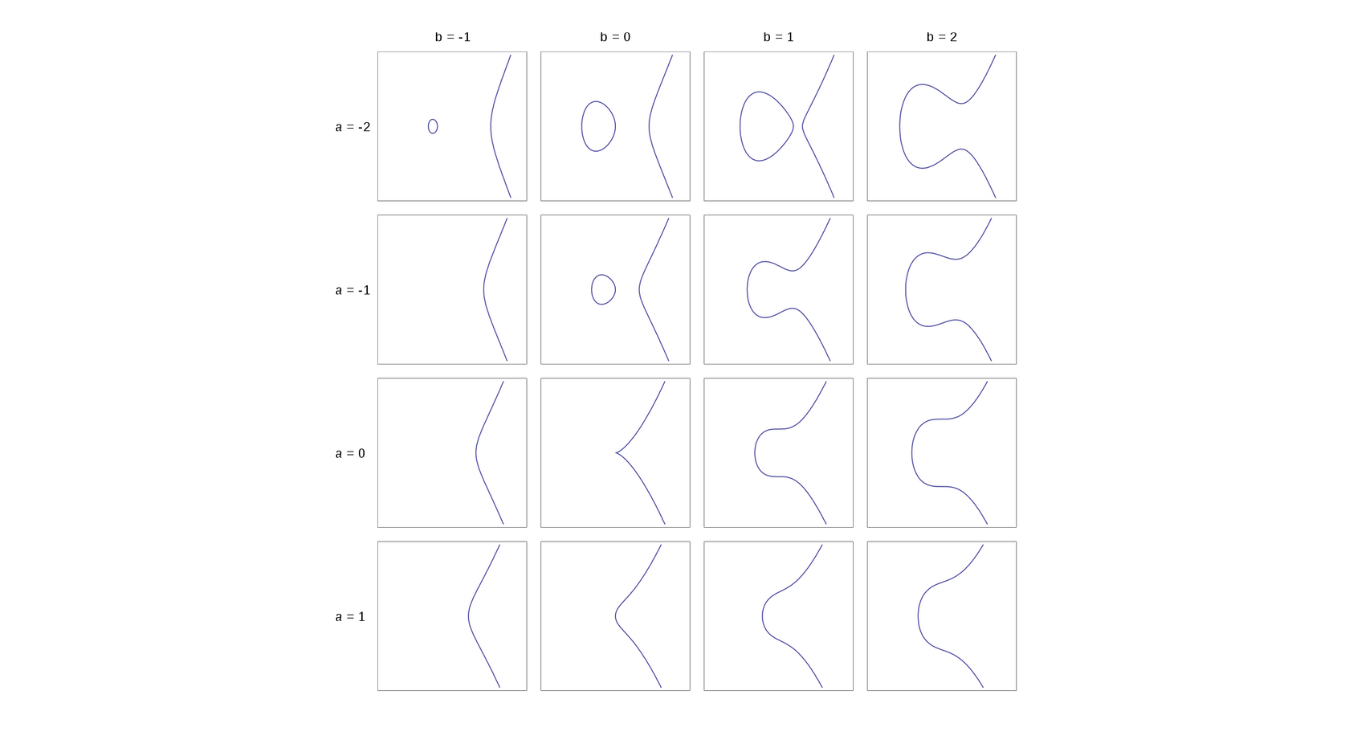
Hình ảnh minh hoạ đường cong elip sưu tầm từ Wiki

Bitcoin sử dụng một đường cong elliptic gọi là Secp256k1. Các đường cong elliptic và mã hóa sử dụng đường cong elliptic có một số tham số, và Secp256k1 có mỗi tham số được xác định. Các giá trị của a và b và hình dạng đồ thị như sau:

a = 0x00000000000000000000000000000000000000000000000000000000000000000 

b = 0x00000000000000000000000000000000000000000000000000000000000000007

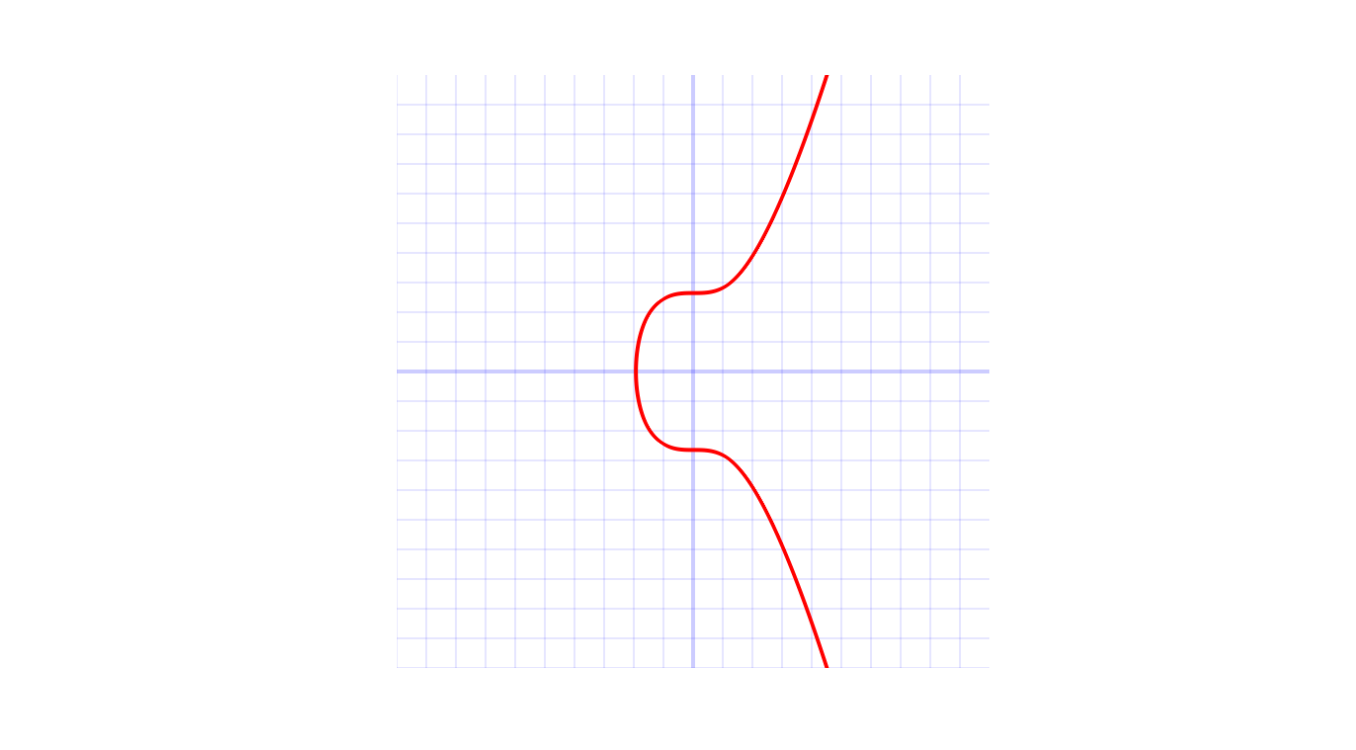
Hình ảnh đường cong Secp256k1 (Nguồn: Wiki)

Tạo public key bằng mật mã đường cong Elliptic 

Từ đây trở đi, chúng ta sẽ đến phần giải thích mã hóa bằng các đường cong elliptic. 

Đầu tiên, mã hóa sử dụng đường cong elip được gọi là mật mã đường cong elip (ECC). Bitcoin sử dụng mật mã này để tạo khóa công khai từ khóa riêng. Một loạt các chữ ký điện tử sử dụng mật mã đường cong elip được gọi là “Thuật toán chữ ký số đường cong elip”. Như tên gợi ý, điều này sử dụng mật mã đường cong elip trong Thuật toán chữ ký số (DSA) và cũng được sử dụng cho chứng nhận kỹ thuật số bitcoin. Các phương trình đường cong elip được sử dụng trong mật mã đường cong elip được sửa đổi một chút so với các phương trình được giới thiệu trước đó. Ở đây chúng ta bắt gặp cụm từ lạ “mod p”. Đây được gọi là phép toán mô đun (hoặc modulo) và đối với “a mod n”, nó đề cập đến phần còn lại của một phép chia cho n. Nói cách khác, phương trình trên có thể được xem là một phương trình trong đó phần dư của vế trái và vế phải bằng nhau. 

Cụ thể, bạn tạo khóa công khai từ khóa riêng bằng cách sử dụng các đường cong elip như thế nào? Thủ tục hơi phức tạp, nhưng nó được tính như sau: 

1. Xác định các tham số đường cong elip p, a, b và điểm quy chiếu G(x, y). Các thông số của Secp256k1 được sử dụng trong Bitcoin như sau: 

     a = 0x00000000000000000000000000000000000000000000000000000000000000000 

     b = 0x00000000000000000000000000000000000000000000000000000000000000007 

     p = 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffc2f 

     Gx = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798 

     Gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8 

     2. Tự thêm G vào G để nhận 2G (bổ sung trong mật mã đường cong elip). 

     3. Lấy giá trị nG bằng cách lặp lại hành động 2. n lần (n: giá trị khóa riêng) 

     4. Đặt nG là giá trị của khóa công khai

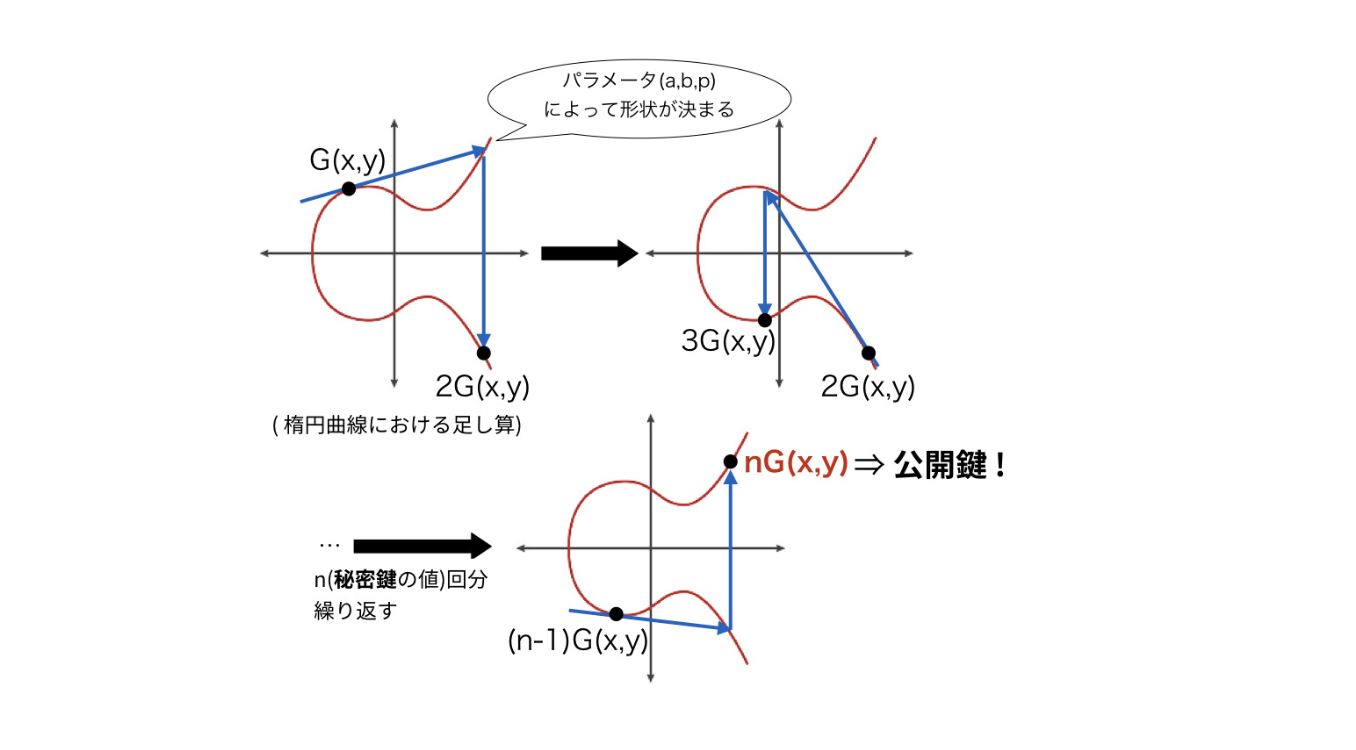
Đồ thị minh hoạ ví dụ 

Ở đây, phép cộng trên đường cong elip khác với phép cộng và phép nhân thông thường. Đầu tiên, đối với điểm tiếp tuyến G trên một đường cong elip nào đó, ta có thể kẻ được đường tiếp tuyến. Tiếp tuyến này luôn cắt một điểm bất kỳ trên đường cong elip không phải là tiếp điểm G. Điểm đối xứng với trục hoành của giao tuyến là tiếp điểm 2G. Hình trên cho thấy quá trình này được lặp lại như thế nào. Do đó, một ví dụ đơn giản về quỹ đạo được nhân lên nhiều lần từ điểm G đến nG được hiển thị bên dưới. 

Như bạn có thể thấy, hình dạng của quỹ đạo rất phức tạp, nhưng có thể tính toán điểm nG được di chuyển n lần từ một điểm G nhất định bằng cách sử dụng máy tính để thực hiện các phép tính tốc độ cao. 

Lưu ý rằng các trục của các đường cong elip mà chúng ta đã thấy cho đến nay là phần còn lại của một điểm (x,y) chia cho p. Điều này là do phần “mod p” trong phương trình trước có hiệu lực. Trong thuật toán mật mã đường cong elliptic, khi đã biết điểm G và p, quy trình tìm điểm tiếp theo được lặp lại n lần để tìm nG. 

Về mặt toán học, có thể dễ dàng lấy được nG từ G bằng cách lặp lại phép toán modulo n lần, nhưng người ta nói rằng rất khó để lấy được n bằng phép toán modulo từ G và nG khi n là một giá trị rất lớn. Điều này được cho là một chiều, giống như hàm băm, và nó có một lợi thế vượt trội là không thể giải mã được mật mã và vì lý do này, nó thường được sử dụng trong mật mã học.

Ứng dụng của đường cong Elliptic

Diffie-Hellman: Giao thức mã hóa công khai cơ bản được đề xuất để chia sẻ khóa bí mật là giao thức Diffie-Hellman. Nếu A (Alice) và B (Bob) ban đầu đồng ý về một đường cong, kích thước trường và loại toán học nhất định. Sau đó, họ phân phối khóa bí mật theo cách sau. Chúng ta có thể thấy rằng tất cả những gì chúng ta cần để xây dựng giao thức Diffie-Hellman là phép nhân vô hướng. 

Thuật toán Chữ ký số Đường cong Elliptic (ECDSA): ECC là một trong những cách tiếp cận triển khai chữ ký số được sử dụng rộng rãi nhất trong tiền điện tử. Để ký các giao dịch, cả Bitcoin và Ethereum đều sử dụng phép nhân nghịch đảo trường, cũng như phép nhân số học, hàm nghịch đảo và phép toán mô-đun. 

Ứng dụng trực tuyến: Bên cạnh đó, ECC không giới hạn đối với tiền điện tử. Đây là một tiêu chuẩn mã hóa sẽ được sử dụng bởi hầu hết các ứng dụng trực tuyến trong tương lai do kích thước khóa và hiệu quả giảm. Được sử dụng phổ biến nhất trong các loại tiền điện tử như Bitcoin và Ethereum, cùng với mã hóa email, dữ liệu và phần mềm một chiều. 

Ứng dụng chuỗi khối: Bitcoin tiền điện tử sử dụng mật mã đường cong elip. Ethereum 2.0 sử dụng nhiều cặp đường cong elip có chữ ký BLS, như đã nêu trong đặc tả BLS do IETF đề xuất, để đảm bảo bằng mật mã rằng trình xác thực Eth2 cụ thể đã thực sự xác minh một giao dịch cụ thể.

Kết luận

Các đường cong elip là một khía cạnh khó khăn trong toán học, nhưng cơ bản thì chúng là các thuật toán tạo khóa công khai an toàn từ khóa riêng của người dùng bằng cách sử dụng toán học mạnh mẽ. Bên cạnh đó trong thời đại công nghệ ngày nay, an toàn thông tin vẫn là một yếu tố hàng đầu nên ECC là một lựa chọn hợp lý thay thế RSA để tạo ra một hệ thống mạng tin cậy hơn cho xã hội. Mong bài viết trên hữu ích với các bạn và hẹn gặp lại các bạn ở bài viết sau của BlockchainWork. 

BlockchainWork biên dịch

      Nguồn: Gaiax Blockchain 

• Tìm hiểu thêm về BlockchainWork tại website: https://blockchainwork.net/
• Ứng viên nắm bắt cơ hội việc làm tại đây: https://blockchainwork.net/candidate-signup
• Nhà tuyển dụng kết nối các tài năng trẻ tại đây: https://blockchainwork.net/employer-signup

>> Có thể bạn quan tâm: 

• Khóa công khai và khóa riêng là gì? 2 loại khóa này khác nhau như thế nào? 
• Chữ ký kỹ thuật số trong blockchain là gì? 5 thuật toán digital signature cần biết
• Khóa công khai và khóa riêng là gì? 2 loại khóa này khác nhau như thế nào?